
ریاضیدان های دانشگاه لیورپول روش خلاقانه جدیدی برای برش پیتزا کشف نموده اند که وقتی از آن مطلع شوید با خودتان فکر می کنید که به هیچ عنوان ارزش این همه تلاش را ندارد.
از منظر این گروه، بهترین راه برای برش پیتزا استفاده از الگوهای پیچیده است که آنها وقت خود را صرف بررسی روش های ممکن آن کرده اند. طریقه ای که توسط monohedral و Stephen Worsley کشف شده بر مبنای تکنیک قدیمی برش به نام Monohedral disc tiling بنا شده و بر اساس آن، این افراد تمامی راه های ممکن برای برش یک دیسک دوبعدی را مورد بررسی قرار داده و در انتها با خود اندیشیده اند که چرا این کشف را روی پیتزا پیاده نکنند؟
این در حالی است که همه ما در دوران تحصیل تصور می کردیم که علم هندسه در خارج از مدرسه هیچ کاربردی ندارد و چرا باید این درس دشوار را پاس کنیم!
بر اساس روش Monohedral disc tiling، یک پیتزا با برش های بلند، به ۶ اسلایس مساوی تقسیم می شود. در فاز دوم، شما می توانید هر کدام از این اسلایس ها را به دو قسمت تقسیم نموده و ۱۲ برش از پیتزا در اختیار داشته باشید، که در این حالت، ۶ اسلایس از آن بخش انتهایی خمیر پیتزا را در خود نخواهند داشت.
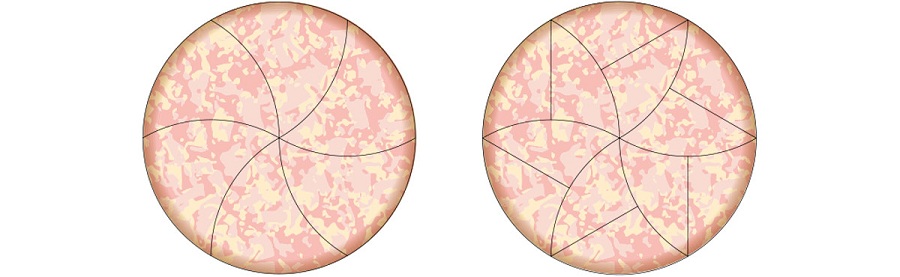
در این رابطه Worsley این طور توضیح می دهد که: «تحقیق ما در واقع پاسخی برای این معمای قدیمی است که یک صفحه گرد مسطح را به چند برش مساوی می توان تقسیم نمود. درست است که پاسخ این معما از قبل وجود داشته اما ما راه حلی کاربردی و کاملا جدید کشف کرده ایم که بر مبنای آن، برخی از تکه ها اصلا به مرکز دیسک وصل نمی شوند.»
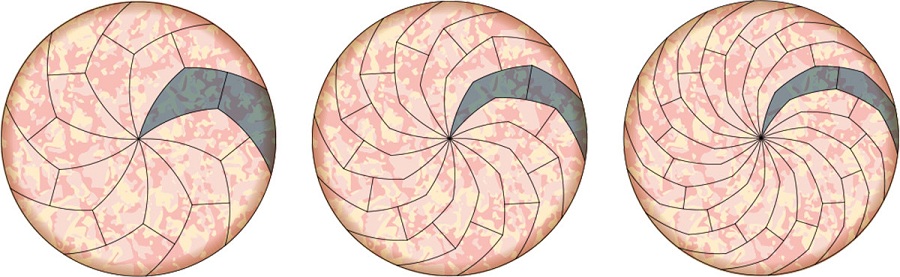
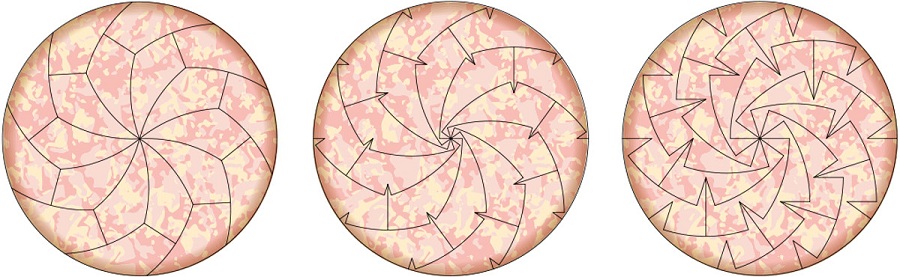
محققان یاد شده کشف کرده اند که می توان یک دایره مسطح را به صورت داسی-شکل و اریب برش داده و برش های متعددی در اختیار داشت که به نام های ۵ گرادیان، ۷ گرادیان و ۹ گرادیان شهرت دارند.
در آخر نیز بد نیست نظر Haddley در مورد این روش برش بگوئیم که اظهار داشته: «از منظر علم حساب،هیچ محدودیتی برای این طرح وجود ندارد، اما لازم به ذکر است که برای طرح های بالاتر از ۹ گرادیان قابل استفاده و کاربردی نیست.»














بدون نظر